• Tweet

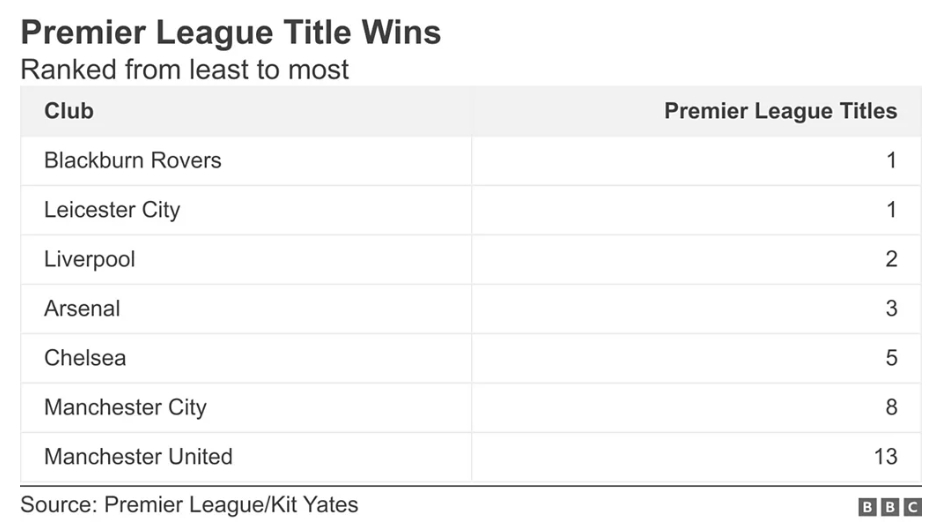
Ceva remarcabil tocmai s-a întâmplat în fotbalul englez. Liverpool FC a fost încoronată campioană a Premier League pentru a doua oară. Adăugat la cele 18 titluri obținute înainte de Premier League, acesta înseamnă că Liverpool egalează acum recordul lui Manchester United, care a fost de 20 de ori campioană a Angliei. Dar în timp ce fanii clubului vor sărbători fără îndoială acest moment de triumf, un alt aspect uluitor al realizărilor lor a atras atenția matematicienilor.

Câștigarea titlului de către Liverpool a completat deschiderea unei serii excepționale de numere care a durat 33 de ani. Secvența apare atunci când o clasăm pe Liverpool alături de celelalte cluburi care au câștigat Premier League de la înființarea acesteia în 1992, enumerându-le după numărul de titluri câștigate, începând cu cel mai mic. După cum se poate vedea în tabelul de mai sus, numărul titlurilor din Premier League este următorul: 1, 1, 2, 3, 5, 8, 13.

Pentru un ochi neavizat, această secvență ar putea să nu pară semnificativă. Dar va fi suficientă pentru a entuziasma mulți pasionați de matematică. Ei o vor recunoaște ca fiind secvența Fibonacci, în care fiecare număr (după primele două) este suma celor două anterioare din secvență. Secvența, daca e reprezentata grafic, poate fi găsită într-o gamă uimitoare de locuri - de la spiralele semințelor de pe capetele de floarea-soarelui și brățările de pe conurile de pin până la modelele arborelui genealogic al unor specii de animale.

Secvențele Fibonacci (secvențe la plural, deoarece începând cu o pereche diferită de numere inițiale și urmând regula adunării numerelor consecutive pentru a genera următoarea secvență, se obține o secvență diferită, dar înrudită) au fost introduse pentru prima dată în știința europeană în 1202 de Leonardo din Pisa, cunoscut și sub porecla Fibonacci (care înseamnă fiul lui Bonaccio).

Cu mult înainte ca Fibonacci să popularizeze secvențele în cartea sa Liber Abaci, totuși, secvențele erau cunoscute de matematicienii indieni. Aceștia se bazaseră pe secvențe pentru a-i ajuta să enumere numărul de poezii posibile de o anumită lungime, folosind silabe scurte de o unitate de durată și silabe lungi de două unități de durată. Poeții/matematicienii indieni știau că se poate face un poem de lungime n luând un poem de lungime n-1 și adăugând o silabă scurtă sau un poem de lungime n-2 și adăugând o silabă lungă. Prin urmare, ei și-au dat seama că, pentru a calcula numărul de poezii de o anumită lungime, trebuie doar să aduni numărul de poezii cu o silabă mai scurte la numărul de poezii cu două silabe mai scurte - exact regula pe care o folosim astăzi pentru a defini o secvență Fibonacci.

În secvențe se ascunde un alt principiu matematic important și înrudit - raportul de aur. Pe măsură ce termenii unei secvențe Fibonacci devin mai mari, raportul dintre fiecare termen și cel precedent se apropie din ce în ce mai mult de raportul de aur - aproximat la 1,61803 prin primele câteva locuri din expansiunea sa zecimală. Se presupune că raportul de aur guvernează dispunerea frunzelor pe tulpina unor specii de plante și că duce la rezultate estetice plăcute atunci când este aplicat în artă, arhitectură și muzică.

Secvențele Fibonacci sunt adesea prezentate de matematicieni ca exemple ale frumuseții matematicii. Ele pot oferi exemple vizuale vii ale matematicii înscrise în tiparele lumii reale, fără de care mulți nematematicieni ar putea avea dificultăți în a înțelege eleganța pe care o vedem în materia noastră. Cu toate acestea, în entuziasmul nostru exagerat de a face prozelitism, există tentația de a prezenta secvențele Fibonacci sau raportul de aur ca un fel de lege naturală atotcuprinzătoare care guvernează fenomene de ordin de mărime, de la formele spiralate ale cochiliilor de nautilus la vârtejurile uraganelor și la brațele curbate ale galaxiilor.

În realitate, deși aceste caracteristici naturale sunt plăcute din punct de vedere estetic, foarte puține dintre ele respectă regulile secvenței Fibonacci sau prezintă raportul de aur. Trebuie să fim atenți să nu încercăm să introducem fiecare model frumos în papucul de sticlă delicat Fibonacci - să sugerăm cauzalitatea și să impunem un sens acolo unde nu există.

Coincidență? Este extraordinar, așadar, ca secvența Fibonacci să apară într-un loc atât de neașteptat precum Premier League. Atunci când, în calitate de oameni de știință, observăm o secvență bine cunoscută ca aceasta apărând aparent din senin, ar trebui să începem să ne întrebăm dacă ne spune ceva important despre procesul care a generat secvența. Există vreun proces surprinzător și nevăzut care stă la baza bătăliilor pentru titlurile din Premier League sau nu este nimic mai mult decât o coincidență drăguță? Doar pentru că putem vedea o secvență Fibonacci în ceva nu înseamnă că este acolo dintr-un motiv anume.

Cu toate acestea, depistarea acestui tip de coincidențe aparente poate fi extrem de utilă pentru procesul de descoperire științifică. În 1912, de exemplu, Alfred Wegener a observat coincidența aparent ciudată că linia de coastă a Africii de Vest și linia de coastă estică a Americii de Sud păreau să se potrivească ca piesele unui puzzle. În ciuda opiniei predominante la acea vreme, conform căreia masele enorme de pământ ale continentelor erau prea mari pentru a se mișca, Wegener a propus singura teorie care îi permitea să își reconcilieze observațiile. Deriva continentală a sugerat că masele de pământ nu erau înrădăcinate în loc, ci își puteau schimba, foarte încet, pozițiile relative pe suprafața Pământului.

Când Wegener și-a publicat teoria în 1915, a devenit de râsul lumii. Geologii au respins ideea sa ciudată, invocând lipsa unui mecanism care să permită deplasarea unor bucăți atât de mari de pe suprafața Pământului, respingând ca o pură coincidență tesselarea aparent confortabilă a continentelor. Cu toate acestea, până în anii 1960, teoria tectonicii plăcilor - mișcarea mantalei solide și a scoarței pe suprafața Pământului - a dat crezare teoriilor lui Wegener, acum acceptate pe scară largă.

Deși coincidențele pot deschide calea către noi descoperiri științifice, ele se pot dovedi, de asemenea, un obstacol în calea progresului științific atunci când par să confirme o teorie incorectă. La începutul anilor 1800, anatomistul german Johann Friedrich Meckel a făcut exact o astfel de greșeală. El credea în scala naturae (scara naturii), în care oamenii se situează deasupra tuturor celorlalte animale într-o ierarhie ordonată, dar statică. Cele mai simple și primitive forme de viață ar fi trebuit să se afle pe cele mai joase trepte ale scării, în timp ce ființele cele mai complexe și avansate se aflau pe cele mai înalte. Opiniile sale nu erau deloc surprinzătoare, având în vedere că acest „mare lanț al ființelor" era teoria predominantă a vremii. Teoria acum general acceptată a „descendenței comune" - conform căreia mai multe specii descind dintr-o singură populație ancestrală - era doar la începuturile sale ca idee la acea vreme.

Meckel a folosit scala naturae pentru a formula o ipoteză cu privire la domeniul său de specialitate - dezvoltarea embrionară. Cunoscută sub numele de teoria recapitulării, aceasta presupunea că, pe măsură ce se dezvoltau, embrionii animalelor de ordin superior (precum mamiferele) treceau succesiv prin forme care semănau puternic cu animalele „mai puțin perfecte", precum peștii, amfibienii și reptilele, aflate pe treptele inferioare ale scării. O predicție surprinzătoare, dar aparent improbabilă, a acestei teorii era că, pe măsură ce oamenii treceau prin „stadiul de pește", embrionii lor ar fi avut fante branhiale.

Întâmplător, în 1827 s-a descoperit că embrionii umani au într-adevăr fante care seamănă cu branhiile într-un stadiu timpuriu de dezvoltare. Această descoperire extraordinară părea să confirme predicția lui Meckel și să coroboreze teoria recapitulării. Dovezile percepute au fost atât de puternice încât teoria a fost acceptată pe scară largă și abia aproape 50 de ani mai târziu, în anii 1870, teoria recapitulării dezvoltării a fost în cele din urmă abandonată definitiv, ideea descendenței comune începând să se impună. Descendența comună stă la baza a ceea ce cunoaștem astăzi drept teoria evoluționistă modernă. Aceasta a clarificat faptul că, departe de a trece printr-un „stadiu de pește" în uter, fantele branhiale au fost o consecință a faptului că, având un strămoș comun cu peștii, împărtășim, de asemenea, o mare parte din ADN-ul și procesele lor timpurii de dezvoltare.

Uneori, coincidențele îi pot deruta pe oamenii de știință, părând să indice o concluzie când, de fapt, există o explicație alternativă pentru observații care este mai bine susținută de fapte. Așadar, ce înseamnă pentru frumosul joc faptul că frumoasa, aproape mistica secvență Fibonacci a apărut în datele privind numărul de titluri câștigate în Premier League? Fără niciun mecanism plauzibil care ar fi putut da naștere secvenței, răspunsul este aproape sigur nimic.

Este minunat să fi descoperit această secvență matematică într-un loc atât de improbabil, oferindu-ne ocazia de a reflecta asupra importanței numerelor Fibonacci. Dar un model nu înseamnă întotdeauna cauzalitate - o coincidență este uneori doar o coincidență. Și, la fel ca fantele branhiale ale lui Meckel, apariția sa în înregistrările Premier League este doar atât - nimic mai mult decât o coincidență spectaculoasă, dar în cele din urmă înșelătoare.